Linear Bounded Automaton

Is it possible to simulate a Linear Bounded Automata with logic circuits where links have min-max bounded delays? I need a reference in the literature. It is not possible to build any interesting memory logic structures (e.g., flip-flops, muller c-element, linear bounded automata,$ dots$). Cc.complexity-theory circuit-complexity turing. A linear bounded automaton, or LBA for short, is a restricted form of a non-deterministic Turing machine with a single tape and a single tape head, such that, given an input word on the tape, the tape head can only scan and rewrite symbols on the cells occupied by the initial input word.

Linear Bounded AutomataThe last machine model of computation which we shall examine is the linearbounded automaton or lba. These were originally developed as models foractual computers rather than models for the computational process. They havebecome important in the theory of computation even though they have notemerged in applications to the extent which pushdown automata enjoy.Here is the motivation for the design of this class of machines. Computers arefinite devices. They do not have unending amounts of storage like Turingmachines. Thus any actual computation done on a computer is not as extensiveas that which could be completed on a Turing machine. So, to mimic (or maybemodel) computers, we must restrict the storage capacity of Turing machines.This should not be as severely as we did for finite automata though. Here is thedefinition. Definition. A linear bounded automaton (lba) is a multi-track Turing machine which has only one tape, and this tape is exactly the same length as the input.That seems quite reasonable. We allow the computing device to use just thestorage it was given at the beginning of its computation. As a safety feature, weshall employ endmarkers (* on the left and # on the right) on our lba tapes andnever allow the machine to go past them. This will ensure that the storagebounds are maintained and help keep our machines from leaving their tapes.At this point, the question of accepting sets arises. Let's have linear boundedautomata accept just like Turing machines. Thus for lba halting meansaccepting.For these new machines computation is restricted to an area bounded by aconstant (the number of tracks) times the length of the input. This is verymuch like a programming environment where the sizes of values for variables isbounded.Now that we know what these devices are, let's look at one. A set which cannotbe accepted by pushdown machines (this is shown in the material on formallanguages) is the set of strings whose length is a perfect square. In symbols thisis: {an n is a perfect square }.

Linear Bounded Automata 2Here is the strategy. We shall use a four track machine with the input writtenon the first track. The second and third tracks are used for scratch work whilethe fourth track is holds strings of square length which will be matched againstthe input string.To do this we need to generate some strings of square length. The second andthird tracks are used for this. On the second track we will build strings of lengthk = 1, 2, 3, and so forth. After each string is built, we construct (on the fourthtrack) a string whose length is the square of the length of the string on thesecond track by copying the second track to the fourth exactly that many times.The third track is used to count down from k. Here is a little chart whichexplains the use of the tracks. track content 1 an (input) ak 2 ak-m amk 3 4Then we check to see if this is the same length as the input. The third track isused for bookkeeping. The algorithm is provided as figure 1.repeat clear the 3rd and 4th tracks add another a to the 2nd track copy the 2nd track to the 3rd track while there are a’s written on the 3rd track delete an a from the 3rd track add the 2nd track's a's to those on 4th trackuntil overflow takes place or 4th track = inputif there was no overflow then accept Figure 1 - Recognition of Perfect Square Length InputsNow we've seen something of what can be done by linear bounded automata.We need to investigate some of the decision problems concerning them. Thefirst problem is the halting problem. Theorem 1. The halting problem is solvable for linear bounded automata. Proof. Our argument here will be based upon the number of possible configurations for an lba. Let's assume that we have an lba with one track (this is allowed because can use additional tape symbols to simulate tracks as we did with Turing machines), k instructions, an alphabet of s

Linear Bounded Automata 3 tape symbols, and an input tape which is n characters in length. An lba configuration is the same as a Turing machine configuration and consists of: a) an instruction, b) the tape head's position, and c) the content of the tape. That is all. We now ask: how many different configurations can there be? It is not too difficult to figure out. With s symbols and a tape which is n squares long, we can have only sn different tapes. The tape head can be on any of the n squares and we can be executing any of the k instructions. Thus there are only k*n*sn possible different configurations for the lba. Let us return to a technique we used to prove the pumping lemma for finite automata. We observe that if the lba enters the same configuration twice then it will do this again and again and again. It is stuck in a loop. The theorem follows from this. We only need to simulate and observe the lba for k*n*sn steps. If it has not halted by then it must be in a loop and will never halt. Corollary. The membership problems for sets accepted by linear bounded automata are solvable. Corollary. The sets accepted by linear bounded automata are all recursive.Let's pursue this notion about step counting a bit more. We know that an lbawill run for no more than k&n&sn steps because that is the upper bound on thenumber of configurations possible for a machine with an input of length n. But,let us ask: exactly how many configurations are actually reached by themachine? If we knew (and we shall soon) we would have a sharper bound onwhen looping takes place. Thus to detect looping, we could count steps with anlba by using an extra track as a step counter.Now let's make the problem a little more difficult. Suppose we had anondeterministic linear bounded automaton (nlba). We know what this is;merely a machine which has more than one possible move at each step. And, ifit can achieve a halting configuration, it accepts. So we now ask: how manyconfigurations can an nlba reach for some input? We still have only k*n*sn

Linear Bounded Automata 4possible configurations, so if we could detect them we could count them usingn tape squares. The big problem is how to detect them. Here is a rather niftyresult which demonstrates nondeterminism in all of its glory. We start with aseries of lemmata. Lemma. Ark survival evolved download gratis. For any nondeterministic linear bounded automaton there is another which can locate and examine m configurations reachable (by the first lba) from some input if there are at least m reachable configurations. Proof. We have an nlba and an integer m. In addition we know that there are at least m configurations reachable from a certain input. Our task is to find them. If the nlba has k instructions, one track, s symbols, and the input is length n, then we know that there are at most k&n&sn possible configurations (Ci) reachable from the starting configuration (which we shall call C0). We can enumerate them and check whether the nlba can get to them. Consider:x=0for i = 1 to k*n*sn generate Ci guess a path from C0 to Ci verify that it is a proper path if Ci is reachable then x = x + 1verify that x ≥ m (otherwise reject)This is a perfect example of the guess and verify technique used innondeterministic operation. All we did was exploit our definition ofnondeterminism. We looked at all possible configurations and countedthose which were reachable from the starting configuration.Note also that every step above can be carried out using n tape squaresand several tracks. Our major problem here is to count to k*n*sn. Weneed to first note that for all except a few values of n, this is smaller than(s+1)n and we can count to this in base s+1using exactly n tape squares.Since we verify that we have indeed found at least m configurations ouralgorithm does indeed examine the appropriate number of reachableconfigurations if they exist.

Linear Bounded Automata 5Lemma. For any nondeterministic linear bounded automaton there isanother which can compute the number of configurations reachable froman input.Proof. As before we begin with an arbitrary machine which has kinstructions, one track, s symbols, and an input of length n. We shalliteratively count the number of configurations (ni) reachable from theinitial configuration. Consider:n0 = 1i=0repeat i=i+ 1 ni = 0 m := 0 for j = 1 to k*n*sn generate Cj guess whether Cj can be reached in i steps or less if path from C0 to Cj is verifiable then ni = ni + 1 if reached in less than i steps then m = m + 1 verify that m = ni-1 (otherwise reject)until ni = ni-1The guessing step is just the algorithm of our last lemma. We do it byfinding all of the configurations reachable in less than i steps and seeingif any of them is Cj or if one more step will produce Cj. Since we know ni-1, we can verify that we have looked at all of them.The remainder is just counting. We do not of course have to save all ofthe ni, just the current one and the last one. All of this can be done on nsquares of tape (and several tracks). Noting that we are done when nomore reachable configurations can be found finishes the proof.Theorem 2. The class of sets accepted by nondeterministic linear boundedautomata is closed under complement.Proof. Most of our work has been done. To build a machine whichaccepts the complement of the set accepted by some nlba involvesputting the previous two together. First find out exactly how manyconfigurations are reachable. Then examine all of them and if any haltingconfigurations are encountered, reject. Otherwise accept.

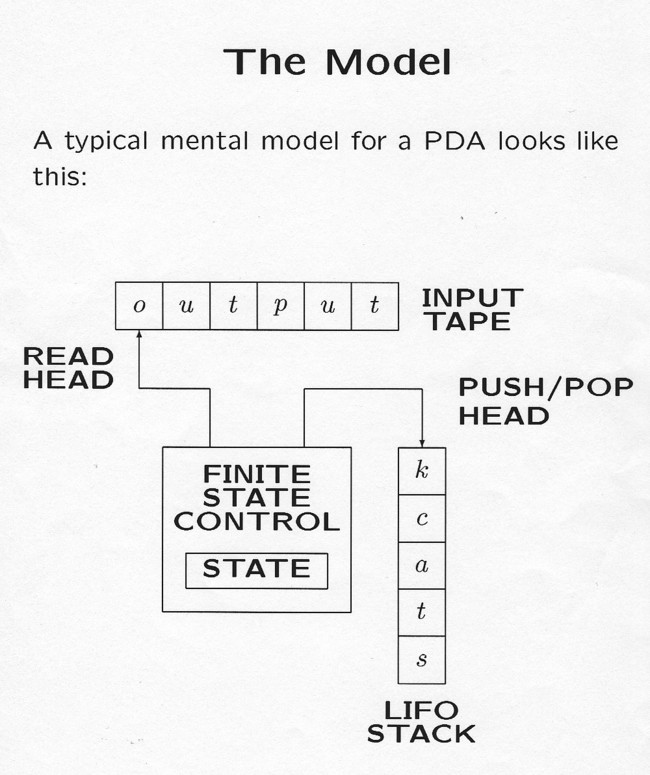
Linear Bounded Automata 6Our final topic is decision problems. Unfortunately we have seen the onlyimportant solvable decision problem concerning linear bounded automata. (Atleast there was one!) The remaining decision problems we have examined forother classes of machines are unsolvable. Most of the proofs of this dependupon the next lemma. Lemma. For every Turing machine there is a linear bounded automaton which accepts the set of strings which are valid halting computations for the Turing machine.The proof of this important lemma will remain an exercise. It should not be toohard to see just how an lba could check a string to see if it is a computationthough. After all, we did a rather careful analysis of how pushdown machinesrecognize invalid computations. Theorem 3. The emptiness problem is unsolvable for linear bounded automata. Proof. Note that if a Turing machine accepts no inputs then it does not have any valid halting computations. Thus the linear bounded automaton which accepts the Turing machine's valid halting computations accepts nothing. This means that if we could solve the emptiness problem for linear bounded automata then we could solve it for Turing machines.In the treatment of formal languages we shall prove that the class of setsaccepted by linear bounded automata properly contains the class of setsaccepted by pushdown machines. This places this class in the hierarchy fa ⊂ pda ⊂ lba ⊂ TMof classes of sets computable by the various machine models we have beenexamining.(By the way, we could intuitively indicate why lba's are more powerful thanpushdown machines. Two observations are necessary. First, a tape which canbe read and written upon is as powerful a tool as a stack. Then, note that apushdown machine can only place a bounded number of symbols on its stackduring each step of its computation. Thus its stack cannot grow longer than aconstant times the length of its input.)The other relationship we need is not available. Nobody knows ifnondeterministic linear bounded automata are more powerful than ordinaryones.